Optimization stream-of-conciousness

In Stanford’s CS231n first module titled: “Optimization: Stochastic Gradient Descent,” they describe how loss for multiclass SVM without regularization is described as:

$$L_i = \sum_{j\neq y_i} \left[ \max(0, w_j^Tx_i - w_{y_i}^Tx_i + 1) \right]$$

For their three-dimensional example across (W). Breaking this down across each row of (W), we get:

$$L_0 = \max(0, w_1^Tx_0 - w_0^Tx_0 + 1) + \max(0, w_2^Tx_0 - w_0^Tx_0 + 1)$$ $$L_1 = \max(0, w_0^Tx_1 - w_1^Tx_1 + 1) + \max(0, w_2^Tx_1 - w_1^Tx_1 + 1)$$ $$L_2 = \max(0, w_0^Tx_2 - w_2^Tx_2 + 1) + \max(0, w_1^Tx_2 - w_2^Tx_2 + 1)$$ $$L = (L_0 + L_1 + L_2) / 3 $$

These can be visualized as the following:

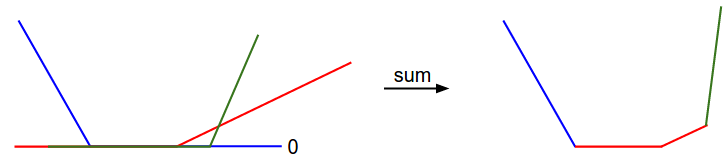
So the thing that I don’t get is… Nope. It all makes sense. I thought they wrote that you could “reorganize” the errors to get a convex shape, however this is wrong – as the giant letters “sum” clearly state. This is a sum of average loss error across all dimensions.

More interesting is this: the graph shown is not differentiable! It is a step-wise function. Mathematically, this isn’t sound, but subgradients still exist.

Other notes from “Optimization: Stochastic Gradient Descent” and “Backprop, Intuitions”:

• the derivative on each vaiable tells you the sensitivity of the whole expression on its value1.
• in the “real-valued circuts” example1, backprop can be thought of as gates communicating to eachother whether they want their outputs to increase or decrease, and how strongly, to make the final output higher.
• backprop in practice should be done while caching forward-pass variables
• gradients add up at forks according to the multivaraite chain rule (states that if a variable branches out to different paths of the circut, then gradients that flow back to it will accumulate via addition).
• “add gates” in a NN distribute gradients evenly to all inputs regargless of forward pass inputs
• “max gates” route the gradient to exactly the maximum input variable.
• “multiply gates” calculate local gradients. In x = 3, y = -4, f(x,y) = x * y == -12, with a gradient of 2, the local gradient for each input is calculated: dx = y*grad == -4 * 2 = -8, dy = x * grad == 3 * 2 = 6
  • as a corollary, this means that small values will get large local gradients and vice-versa. This makes sense as the local gradients move variables them towards a common gradient. This makes preprocessing and initial weights very important. For more on initial weights, see Xavier initialization.
• for vectorized optimizations we do the same as with scalars, but we have to pay attention to dimensionality and transpose operations.
  • tensor-tensor multiply gradients (including matrix-matrix, matrix-vector, and vector-vector) are dot products as forward passes and transpose dot products for gradients. Paying attention to input dimensionality and ensuring that gradient dimensions match is very important.