Kolmogorov–Smirnov
A cumulative distribution function (CDF) is the theoretical function which will tell you that some random variable can be found with a probability less than or equal to some value, p - which is normally found on the y-axis. The empirical cumulative distribution function (or EDF), on the other hand, is just your observed CDF. Where CDFs increment in steps of 1/n for an n-sized sample, an EDFs is usually much more sporadic, taking on the look of a step function with the horizontal sections representing where your data is most sparse.
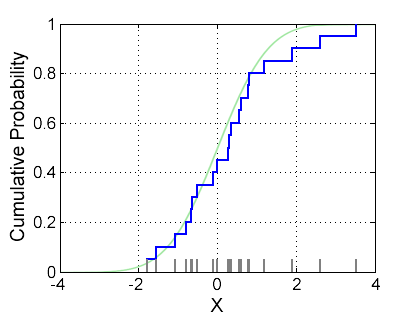
One measure that we are using in CSSR is a two-sided Kolmogorov-Smirnov test, or a KS test for short. The underlying principle is that a KS test will compare the EDF of your sample to a reference; which could be the CDF of a reference distribution or the EDF of your second sample, depending on if your test is one- or two- sided.
The KS statistic quantifies the maximum possible difference between probabilities of the sample and reference. From what I can tell, the two-sample KS test is one of the most useful, and general, nonparametric methods since we can draw comparisons of any two samples purely on what we observe. Because we are looking at largest differences, what we measures is sensitive to location within the distribution, as well as the shape – the more sparse the dataset in regions that are more pertinent (not the extremes), the worse off your statistic.

Since a two-sample KS test only checks if the samples come from the same distribution, we don’t necessarily know what that distribution is. For this purpose, there are tables of critical values which you can use to find out if the data you have is normally distributed, or not. One of these tables you can find here.
Journal section, for anyone interested in the status of my research:
Switching tracks to the status of CSSR, I think I did pretty good job getting a prototype out the door. Of course the thing is pretty buggy, but for never having touched scala in such a long time, I’m pretty proud happy with how easy it was to come up with a clean solution while taking advantage of a number of scala features (as well as a matrix library). Perhaps if things go well I might have time to introducing scalaz… however testing, as well as a Viterbi implementation (as a part of some knowledge dives), stand in the way of that. Primarily, I’ve been investigating the KS test was imperative since we have our own KS test implemented, ported from Numerical Recipes in C: The Art of Scientific Computing, and I’d like to have it tested.